Post-quantum cryptography world: What is it like to live in it?

Rising quantum computer development worries the crypto industry. We explore its impact, causes, and actions taken against this threat.
Post-quantum cryptography has become a major concern for the cryptocurrency sector and other industries due to the slow yet steady development of quantum computers. In this article, you will learn about the problem, its origin, mechanisms, and implications, as well as the steps being taken to address the threat posed by quantum computers.
Table of Contents
What is post-quantum cryptography (PQC)?
Post-quantum cryptography refers to the study of cryptographic algorithms that are considered able to withstand an attack by quantum computers. These cryptographic algorithms are usually public-key algorithms and are sometimes called quantum-proof, quantum-safe, or quantum-resistant algorithms.
Quantum-proof cryptography has become a significant issue for the cryptography sector as computer scientists continue to work on developing quantum computers. These types of machines make use of the quantum states of subatomic particles to store information. In quantum computers, calculations are based on the behavior of particles at the atomic and sub-atomic level, hence the name quantum.
Quantum computers are able to handle a much higher number of instructions per second than previous machines. The exponential increase in the millions of instructions per second (MIPS) is because data in a quantum computer exists in more than one state. This is contrary to regular computers, such as a typical PC, which are binary.
Because data in quantum computers is not binary, the machine can process multiple options at the same time. The simultaneous exploration of different end states from the same set of particles, variables, or data allows quantum computers to offer much faster processing capabilities. In quantum computers, data is represented by qubits, which differ significantly from the bits in classical computers.
Unlike bits that are binary and can be either 0 or 1, qubits utilize the principles of quantum superposition and entanglement. This means a qubit can represent both 0 and 1 at the same time to varying degrees, allowing the computer to process a multitude of potential outcomes simultaneously. The complex nature of qubits, derived from these quantum properties, is what potentially gives quantum computers their superior processing power in some applications.
How does PQC work?
Classical encryption methods rely on the computational difficulty of problems like factoring large prime numbers or computing discrete logarithms. The security of these methods lies in the extensive time and resources classical computers require to solve these problems. Quantum computers can use algorithms like Shor’s to reduce this time significantly.
Post-quantum cryptography (PQC) is premised on computational problems that are challenging for both classical and quantum computers to solve. These include but are not limited to, lattice-based problems, systems of multivariate polynomials, error-correcting codes, and supersingular elliptic curve isogenies. The complexity of these problems lies in their mathematical structure, which is resistant to the speedup provided by quantum computers’ ability to process multiple states simultaneously.
By focusing on these hard-to-solve problems, PQC aims to establish a robust security framework resilient against the potential future capabilities of quantum computing. This proactive approach is crucial for preemptively protecting sensitive data and communications against the evolving landscape of computational power.
Potential post-quantum algorithms
Lattice-based cryptography: Lattice-based cryptography is one of the most promising and versatile approaches to PQC. The security of lattice-based schemes relies on the hardness of problems related to the geometry of high-dimensional lattices — structures consisting of points at regular intervals in multiple dimensions.
One of the most famous problems in this domain is the Shortest Vector Problem (SVP), which is believed to be hard for both classical and quantum computers. Algorithms like CRYSTALS-Kyber and CRYSTALS-Dilithium, which were selected by the NIST for standardization, fall under this category. These algorithms are not only resistant to known quantum attacks but also offer efficiency and practicality, with relatively small key and ciphertext sizes compared to other PQC methods.
Code-based cryptography: This approach has its roots in error-correcting codes, which are used to detect and correct errors in data transmission. The security of code-based systems typically relies on the hardness of decoding a random linear code, which remains a difficult problem even for quantum computers.
The most well-known algorithm in this category is the McEliece cryptosystem, which has been studied for decades and has withstood all known attacks, classical and quantum alike. However, one of the drawbacks of code-based cryptography is the large key sizes, which can be impractical for certain applications.
Multivariate quadratic equations: Cryptosystems based on multivariate quadratic (MQ) equations involve finding solutions to systems of quadratic equations over a finite field. The security of these systems is derived from the MQ Problem, which is to solve a set of multivariate quadratic equations and is considered hard for both classical and quantum computers.
Algorithms like Rainbow and GeMSS are based on this approach. While they offer relatively fast encryption and decryption times and have smaller key sizes than code-based systems, the security level per key size bit is not as high as that of lattice-based cryptography.
Hash-based cryptography: Hash-based cryptography is another promising direction for PQC. These schemes use secure hash functions — functions that take an input and return a fixed-size string of bytes that appears random. The security of hash-based schemes relies on the collision resistance of the hash function, which remains a hard problem in the quantum setting.
The SPHINCS+ algorithm is an example of a hash-based signature scheme that provides strong security guarantees and has been selected by NIST for further consideration. However, hash-based signatures typically have larger signatures than other PQC methods.
Isogeny-based cryptography: Isogeny-based cryptography is a more recent area of research and is based on the mathematical structure of elliptic curves. It involves computing functions (isogenies) that map between different elliptic curves. The security relies on the difficulty of finding the isogeny between two elliptic curves given only their public descriptions.
The Supersingular Isogeny Key Encapsulation (SIKE) is an example of an isogeny-based cryptosystem. While it offers very small key sizes and is believed to be secure against both classical and quantum attacks, it’s relatively new and not as well-understood or tested as other methods.
An emerging threat
Due to their processing speed, quantum computers may represent a risk for many cryptography-based applications.
In 2014, after Edward Snowden’s leak revealed a significant amount of classified information, the public learned about the NSA’s quantum computing project, known as “Penetrating Hard Targets,” which was funded with a $79.7 million budget and is believed to be based in College Park, Maryland. While this development raised some concerns, the relatively modest budget and the project’s nascent stage led to a subdued reaction from the industry.
The concerns intensified in 2015 when the NSA released new guidelines, prompting governmental and private entities to transition to quantum-resistant cryptography. The NSA articulated its goal to ensure cost-effective security against potential quantum computer threats by collaborating with various stakeholders to develop a robust suite of quantum-resistant algorithms.
These announcements led to widespread speculation in the cryptography community. Some wondered if the NSA had made significant strides in quantum computing, perhaps even achieving stable qubits and a functional quantum computer. Others speculated that while the NSA might not have developed a quantum computer, it could have insights into the progress of quantum computing elsewhere.
This situation underscores the secretive and speculative nature of quantum computing in the context of national security and the global race toward quantum supremacy. The NSA’s involvement highlights the strategic importance of quantum-resistant cryptography as a defense against the potential future capabilities of quantum computing.
One significant challenge posed by quantum computing is related to Shor’s algorithm, named after mathematician Peter Shor, who devised it in 1994. This algorithm is designed specifically for quantum computers and can efficiently factorize large numbers into their prime components in polynomial time — a task that is extremely time-consuming for classical computers.
However, it’s important to note that not just any quantum computer can effectively run Shor’s Algorithm. The quantum computer needs a sufficient number of stable, error-corrected qubits to handle complex operations without losing coherence, which is a significant technical hurdle yet to be fully overcome. As of now, such quantum computers are still in the developmental stages.
The potential of Shor’s algorithm to quickly uncover the prime factors of large numbers underpins the quantum threat to encryption techniques. This capability is particularly concerning for systems relying on the difficulty of prime factorization for security, such as RSA, which is prevalent in cryptography and, by extension, the cryptocurrency sector.
Using Shor’s algorithm, quantum computers can wreak havoc on all public key systems currently in use. This is because if one has access to a powerful quantum computer and the public key, they could potentially decipher the prime factorization. Much of the Internet uses RSA, a type of public-key cryptosystem, to securely transmit data. RSA stands for Rivest–Shamir–Adleman, after the scientists who created it. The cryptosystem consists of two components, the public key and the decryption key which is hidden from the public.
Using the public key and Shor’s algorithm, quantum computers are theoretically able to break RSA encryption. Quantum computing is also thought to be ready to tackle other mathematical problems that classical computers require significant resources to break. Conventional computers are unable to crack many of the algorithms in use today because they would require large amounts of power to do so. The amount of energy needed to achieve this end is unfeasible and negates any of the risks posed by classical computers.
On the other hand, quantum computers could crack public key encryption in much less time and compute discrete logarithm mod primes and discrete logs over elliptic curves. Quantum computing poses a risk to the cryptocurrency industry because the machines can be used to break the digital signatures utilized to ascertain transactions in digital currencies. The implication of this is immense as it can allow double spending, theft, and forgeries and can likely result in the downfall of the affected cryptocurrency.
If we had a quantum computer with enough error-corrected qubits, Shor’s algorithm, in theory, could be used to break the cryptographic schemes used in Bitcoin. In April 2022, a study by Deloitte showed that in such a case, around one-quarter of the bitcoin in circulation would be in danger.
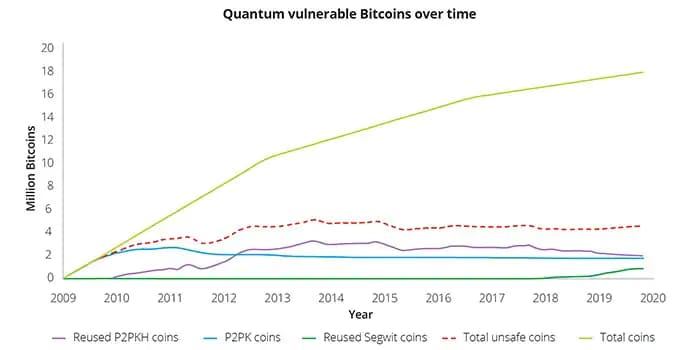
However, researchers suggest that maintaining reliable quantum computing performance remains challenging. This is because quantum computers, under the slightest disturbances such as electrical discharges or stray electromagnetic fields, can lose their quantum states, a process known as decoherence. This doesn’t mean they start functioning like classical computers, rather, their computational advantage deteriorates significantly, resulting in high error rates.
Robert Schoelkopf, a Yale professor and founder of a company called Quantum Circuits, explains the promise and challenge of creating functional quantum computers. Schoelkopf says:
“If you had 50 or 100 qubits and they really worked well enough, and were fully error-corrected—you could do unfathomable calculations that can’t be replicated on any classical machine, now or ever. The flip side to quantum computing is that there are exponential ways for it to go wrong.”
For these reasons, many consider quantum computers to be far from ready and a theoretical threat at this point. However, technology giant IBM plans to produce quantum computers with more than 4,000 qubits by 2025.
While there is much speculation about the potential impact of fully functional quantum computers on digital currencies and other cryptographic systems, the actual current state of quantum computing technology is less advanced. Israeli cryptographer Adi Shamir, the “S” in the RSA algorithm, shared his relatively sanguine outlook at the 2017 RSA conference:
“I wouldn’t lose too much sleep over quantum computers. Quantum computers are not at the top of my list of worries. I think there is a higher chance that RSA could be broken by a mathematical attack.”
Indeed, while the prospect of quantum computing poses theoretical concerns for various sectors, it’s important to note that practical and scalable quantum computing remains an aspirational goal. At the 2017 RSA conference, U.S. Rep. Michael McCaul, R-Texas, emphasized the U.S.’s commitment to developing policies and strategies to bolster security against the potential future threat of quantum computers.
As the House Homeland Security Committee chairman and a co-chair of the Cybersecurity Caucus, McCaul advocated for increased investment in research, underlining the importance of global collaboration in preparing for a future where quantum computing is a reality. His remarks underscore the importance of proactive preparation but also implicitly acknowledge that the era of practical quantum computing has not yet arrived.”
NIST guidance
In December 2016, NIST launched a post-quantum crypto project designed to identify quantum-resistant public-key cryptographic algorithms. The National Institute of Standards and Technology (NIST) is a non-regulatory agency of the United States Department of Commerce whose mission is to promote innovation and industrial competitiveness through science and innovation.
NIST provides industry standards concerning a number of technological innovations including cryptography. Using the submissions received in the post-quantum crypto project, NIST plans to issue guidance in a few years regarding how to proceed in a reality where quantum computers exist.
However, this process is expected to take a long time. Sufficiently testing algorithms requires adequate peer review which can be time-consuming in and of itself. This procedure is part of what makes modern public key infrastructure so robust. Shamir explains:
“Remember, we are celebrating this year the 40th anniversary of the RSA algorithm; it was invented in 1977. Should we switch now, as a cautionary step, to a quantum-resistant algorithm? If someone would come up with something that is both quantum-resistant and better than our current algorithms, we win.”
FAQs
Does post-quantum cryptography exist?
Yes, post-quantum cryptography (PQC) exists. It refers to cryptographic algorithms specifically designed to resist attacks from quantum computers. These algorithms are being developed to ensure the security and integrity of digital communications in a future where quantum computers may render current encryption algorithms vulnerable.
What is the difference between QKD and post-quantum cryptography?
Quantum Key Distribution (QKD) and post-quantum cryptography serve different purposes. QKD is a method of securely distributing encryption keys using quantum properties, whereas post-quantum cryptography focuses on developing encryption algorithms that can withstand attacks from quantum computers. QKD ensures secure key distribution, while post-quantum cryptography addresses the threat posed by quantum computers to existing encryption systems.
Are current cryptographic algorithms vulnerable to quantum attacks?
Yes, quantum computers have the potential to compromise the security of current cryptographic algorithms. They could leverage algorithms like Shor’s algorithm to pose a threat to widely used public-key encryption algorithms, such as RSA. However, executing such attacks would require a quantum computer with significant computational power, which currently doesn’t exist.
How do quantum computers pose a threat to current cryptographic systems?
Quantum computers could pose a threat to current cryptographic systems because they may be able to break the underlying mathematical problems that encryption algorithms rely on. Algorithms like Shor’s algorithm, if executed on powerful quantum computers, could solve these problems, rendering current encryption algorithms vulnerable and compromising the security of sensitive data.
How will the transition to post-quantum cryptography impact existing systems and infrastructure?
The transition to post-quantum cryptography will require updating existing systems and infrastructure to incorporate quantum-resistant algorithms. This will involve implementing new cryptographic protocols and updating software and hardware components to support these algorithms. The transition may also bring challenges in making different systems work together and ensuring that older systems can still communicate securely with the new post-quantum cryptography systems.
How can I ensure that my sensitive data remains secure in a post-quantum world?
To ensure the security of important data in a post-quantum world, there are several measures you can take. First, start considering the implementation of post-quantum cryptographic algorithms and protocols. Additionally, you can strengthen your security by extending the lengths of asymmetric keys and utilizing symmetric cryptography whenever possible. By using longer keys, you can stay ahead of early versions of error-corrected quantum computers, as breaking these longer keys would require a significantly higher number of qubits.
Stay informed about the latest developments in post-quantum cryptography and follow recommended security guidelines