Game Theory in Cryptoeconomics

Bitcoin’s pseudonymous creator(s) Satoshi Nakamoto utilized a range of scientific and economic models when he developed the world’s first digital currency. While many of these technologies already existed, it was Nakamoto’s combination of this knowledge – in conjunction with his developed distributed ledger technology (DLT) – that ushered in a new age of decentralized digital currencies.

Polymath a Prerequisite

Nakamoto amalgamated cryptography, computer science, and economic models to create a network that would function effectively in a decentralized manner, with individuals acting in their best interest yet still upholding the integrity of the network. Nakamoto was able to do this by employing principles already developed in a branch of science called game theory.

After publishing his white paper and subsequently creating the Bitcoin ecosystem upon mining the genesis block, Nakamoto proved the viability of his hypothesis. Following the continued growth of the cryptocurrency, developers have continued to base and/or improve on Bitcoin’s foundation resulting in a vast number of altcoins.

Game theory plays an essential part in the cryptocurrency economy as it is the basis upon which developers are able to predict the outcomes of their networks effectively. This article explores hows game theory keeps decentralized cryptocurrency networks functioning effectively and its importance in the crypto economy as a whole.

What Is Game Theory?

Game theory is a branch of study that investigates how individuals interact with each other and how they make decisions in a specific setting. In his 1991 book “Game Theory: Analysis of Conflict,” Roger Myerson described it as “the study of mathematical models of conflict and cooperation between intelligent rational decision-makers.”

The esteemed mathematician

1/ The crypto education thread: I get asked constantly for educational resources and it's tough – have to follow a "spiral", circling around the fields that contribute to cryptocurrency understanding, with each gradually making more sense relative to your knowledge of the others. pic.twitter.com/aEc8vLdJEL

— Ari Paul ⛓️ (@AriDavidPaul) May 20, 2018

The esteemed mathematician John von Neumann created game theory. Neumann was an Austrian-Hungarian scientist who is credited with a number of discoveries in the areas of mathematics, physics, computer science, economics, and statistics. The scientist published over 100 papers in his lifetime and his works are widely cited, having implications in many industries and fields of study. He is widely considered to be one of the best mathematicians of the last century.

In 1928, Neumann established that two individuals interacting with each other each had a set of actions that would prove to be the option with the least loss for them. This is called the Minimax Theorem. The theory is defined as “a theorem in the theory of games where the lowest maximum expected loss equals the highest minimum expected gain.” This is considered to be the birth of game theory.

While working on the Minimax Theorem, Neumann only considered two person scenarios. However, in 1944 he published a book called “The Theory Of Games And Economic Behavior” in which he outlined more complex situations involving a greater number of players as well as other factors that could affect the outcome. Mathematician Oskar Morgenstern co-authored the book.

Initially created as a mathematical model designed to have implications on economics especially in the context of markets such as oligopolies, game theory has been used to anticipate the actions of rational decision makers in biology, psychology, politics, and computer science. As a result, the concept is now an umbrella term that refers to the study of rational decision making.

The Components of Game Theory

In the context of game theory, a game is the interaction of two or more players where their decisions affect each other. It is defined as “a situation involving a set of players who each have a set of possible choices, in which the outcome for any individual player depends partially on the choices made by other players.” It does not refer to games played for entertainment purposes though it is important to note that these games do utilize aspects studied within the confines of game theory.

Players are the decision makers in the game. These are assumed to be rational and interested in establishing outcomes that involve the best possible circumstance for themselves. Players will make decisions while considering the approach that will result in positive outcomes for themselves. This is referred to as the strategy. Lastly, once the players have employed their chosen strategy, the resulting scenario is known as the payoff.

Game theory is based on studying these three aspects: The decision makers, the strategy, and the payoff. When identifying the best possible decisions, especially in a two-player game, the available options are represented in a table known as the payoff matrix.

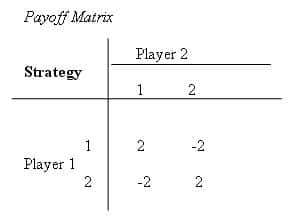
The Types of Games

There are five main games in the context of game theory. Cooperative and non-cooperative games are those in which players may or may not agree to work together to achieve the best possible outcomes for themselves. Non-cooperative games are believed to showcase the most accurate results as players within them are more likely to analyze the situation profoundly.

Concerned with defining games based on players knowledge of the opponents’ strategies, there are also simultaneous-move games and sequential move games.

Simultaneous move games are those in which players make their decisions at the same time. Additionally, a game can also be simultaneous if the players are unaware of the others move because the lack of knowledge effectively renders all decisions simultaneous as they are not affected by the others’ choices. Conversely, sequential move games are those in which players are aware of the options or strategies of their opponents.

In defining the decision-making strategies of players, there are two scenarios. These are standard form games and extensive form games. Normal form games are those whose payoff matrices can be represented in the form of a table. Extensive form games are those more complex scenarios in which decisions are described in the form of a tree.

(Source: YouTube)

In regards to outcomes, there are constant sum, zero-sum, and non-zero sum games. A constant sum game is a game in which the sum of the result of all players’ decisions remains constant even if outcomes are different. Conversely, a zero-sum game is a type of content sum game in which the outcomes of all players are zero. In a zero-sum game, the applied strategies of each player cannot affect the resources available in the game.

Additionally, in a zero-sum game, the gain of one player is always equal to the loss of the other player in the game. A non-zero sum game, on the other hand, is a game in which the sum of the outcomes of all involved players is not zero.

Lastly, there are symmetric and asymmetric games. These concern the strategies players can employ. If all available options to all players are the same, then it is a symmetric game. Asymmetric games are therefore the opposite. Symmetric games are only feasible in the short-term as with a larger time window the complexity increases as more choices become available to players.

The Nash Equilibrium

One of the most critical concepts in game theory is the Nash Equilibrium. It is named after well-respected mathematician John Nash who defined it. The Nash Equilibrium refers to a solution concept in which a two or more player game has an outcome where players will have no incentive to change their decision if they were to find out the choices of their opponents. This is because the players have already made the best possible choice for themselves. According to Investopedia:

“The Nash Equilibrium is the solution to a game in which two or more players have a strategy, and with each participant considering an opponent’s choice, he has no incentive, nothing to gain, by switching his strategy. In the Nash Equilibrium, each player’s strategy is optimal when considering the decisions of other players. Every player wins because everyone gets the outcome they desire. To quickly test if the Nash equilibrium exists, reveal each player’s strategy to the other players. If no one changes his strategy, then the Nash Equilibrium is proven.”

The scenario outlined by Nash is one in which players act in their best interest at all times.

Interestingly, they do not do this because of external influence or coercion, instead due to self-preservation: “Practically speaking, a Nash equilibrium is a law that no one has incentive to break even in the absence of an effective police force. In a sense, these laws are self-enforcing. Following traffic signals is an example of Nash equilibrium at work. When another car is speeding toward you, you do not stop at the red light because a police officer will give you a ticket if you go. You stop because you do not want to die.”

Considering the Prisoner’s Dilemma, a type of well-known example of a non-cooperative game which is used to understand the workings of the Nash equilibrium. It becomes apparent that sometimes the best actions for the individual are not the best for the society as a whole. This introduces the concept of punishment into the game model. The idea of punishment can be represented in the payoff matrix, and it has effects on the choice which is the best for all players, that is the point at which the Nash Equilibrium lies.

Another important solution concept is the Grim Trigger equilibrium. It refers to a game where players are incentivized to stay cooperative with each other for as long as they all continue to act in this manner. As soon as one player acts in an uncooperative manner, this is a trigger for a cycle of discord across the game. All players will defect, and continue to do so, once one player defects. Thus, the fear of a completely discordant scenario keeps players from behaving dishonestly.

How Does Game Theory Affect the Cryptocurrency Economy?

Cryptoeconomics is the study of how cryptographic tools can be used to create economic incentives. The blockchain, as in the Bitcoin Network, is a self-enforcing Nash Equilibrium. In combination with cryptography, Nakamoto used game theory to build a network where the players were incentivized to act, and continue operating, in a way that resulted in net positive outcomes for the whole ecosystem.

Within a blockchain, miners validate transactions in the network and as a result, are rewarded with new units of the currency in question. While honest miners are essential to keep a system in proper functioning order, dishonest miners can destroy a network. However, due to the inherent design of the blockchain, miners are incentivized to stay honest.

3/ Bitcoin's mining is relatively centralized, GPU mining is insecure from a game theory perspective, even the simplest ethereum smart contracts written by credible devs are very often buggy.

— Ari Paul ⛓️ (@AriDavidPaul) March 8, 2018

Blockchain protocols specify that any block mined on top of an invalid block itself becomes invalid. This means that miners will avoid any invalid block, such as one used in a double spend or any other dishonest activity. The best outcome for any miner is continuing to mine on the right chain as this is where he or she stands the best chance of gaining new bitcoins.

The two players in a (Proof of Work) blockchain are the miners and the users. Miners stay honest because they want to stay within the confines of the Nash Equilibrium. Users, however, will continue to use the right chain, instead of deviating to another shorter chain, because of a combination of two factors.

The Schelling Point refers to a focal point which players are most likely to refer to or prefer in a game. In the context of a blockchain, users will choose the honest chain because they know it better. Additionally, the concept of bounded rationality also affects how users choose a chain. This concept refers to the fact that players will always take the path of least resistance available to them. This means they will most likely choose what they are used to accepting.

Lastly, the unlikely though theoretically possible scenario that a large enough group of dishonest miners were able to collude and overpower the honest miners to take over a blockchain is mitigated by the Grim Trigger equilibrium. This is because the dishonest miners would keep overpowering whatever group was in control of the blockchain. Due to this lack of stability as well as the probable fall in the value of the digital currency, miners are incentivized to stay honest.